Bhaskara - biografia
Bhaskara viveu de 1114 a 1185 aproximadamente, na Índia. Nascido numa tradicional família de astrólogos indianos seguiu a tradição profissional da família, porém com uma orientação científica, dedicando-se mais à parte matemática e astronômica (tais como o cálculo do dia e hora da ocorrência de eclipses ou das posições e conjunções dos planetas) que dá sustentação à Astrologia. Seus méritos foram logo reconhecidos e muito cedo atingiu o posto de diretor do Observatório de Ujjain, o maior centro de pesquisas matemáticas e astronômicas da Índia, na época.
Seu livro mais famoso é o Lilavati, um livro bem elementar e dedicado a problemas simples de Aritmética, Geometria Plana (medidas e trigonometria elementar) e Combinatória. A palavra Lilavati é um nome próprio de mulher (a tradução é Graciosa), e a razão de ter dado esse título a seu livro é porque, provavelmente, teria desejado fazer um trocadilho comparando a elegância de uma mulher da nobreza com a elegância dos métodos da Aritmética. Numa tradução turca desse livro, 400 anos depois, foi inventada a história de que o livro seria uma homenagem à filha que não pode se casar. Justamente essa invenção é que tornou-o famoso entre as pessoas de pouco conhecimento de Matemática e de História da Matemática. Parece, também, que os professores estão muito dispostos a aceitarem estórias românticas em uma área tão abstrata e difícil como a Matemática; isso parece humanizá-la mais. Ele escreveu um livro muito importante, que é:
Equações INDETERMINADAS ou diofantinas:
Chamamos assim às equações (polinomiais e de coeficientes inteiros) com infinitas soluções inteiras, como é o caso de:
y - x = 1 que aceita todos os x = a e y = a + 1 como soluções , qualquer que seja o valor de a
a famosa equação de Pell x2 = N y2 + 1
Bhaskara foi o primeiro a ter sucesso na resolução dessa equação, para isso introduzindo o método do chakravala (ou pulverizador).
Equações INDETERMINADAS ou diofantinas:
Chamamos assim às equações (polinomiais e de coeficientes inteiros) com infinitas soluções inteiras, como é o caso de:
y - x = 1 que aceita todos os x = a e y = a + 1 como soluções , qualquer que seja o valor de a
a famosa equação de Pell x2 = N y2 + 1
Bhaskara foi o primeiro a ter sucesso na resolução dessa equação, para isso introduzindo o método do chakravala (ou pulverizador).
EXEMPLO: para resolver as equações quadráticas da forma ax2 + bx = c, os indianos usavam a seguinte regra:
“multiplique ambos os membros da equação pelo número que vale quatro vezes o coeficiente do quadrado e some a eles um número igual ao quadrado do coeficiente original da incógnita. A solução desejada é a raiz quadrada disso.”
É também muito importante observar que a falta de uma notação algébrica, bem como o uso de métodos geométricos para deduzir as regras, faziam os matemáticos da Era das Regras terem de usar varias regras para resolver equações do segundo grau. Por exemplo, precisavam de regras diferentes para resolver x2 = px + q e x2 + px = q. Foi só na Era das Fórmulas que iniciaram as tentativas de dar um procedimento único para resolver todas as equações de um grau dado.
Bhaskara conhecia a regra acima, porém, a regra não foi descoberta por ele. A regra já era do conhecimento de, no mínimo, o matemático Sridara, que viveu há mais de 100 anos antes de Bhaskara.
O hábito de dar nome de Bhaskara para a fórmula de resolução da equação de 2º grau se estabeleceu no Brasil por volta de 1960. Esse costume, aparentemente só brasileiro ( não se encontra o nome de Bhaskara para essa fórmula na literatura internacional), não é adequado pois :
* Problemas que recaem numa equação de 2º grau já apareciam, há quase 4.000 anos atrás, em textos escritos pelos babilônicos. Nestes textos o que se tinha era uma receita ( escrita em prosa, sem uso de símbolos) que ensinava como proceder para determinar as raízes em exemplos concretos com coeficientes numéricos
* Até o fim do século 16 não se usava uma fórmula para obter as raízes de uma equação do 2º grau, simplesmente porque não se representavam por letras os coeficientes de uma equação. Isso só começou a ser feito a partir da François Viéte, matemático francês que viveu de 1540 a 1603.
Logo, embora não se deva negar a importância e a riqueza da obra de Bhaskara, não é correto atribuir a ele a conhecida fórmula de resolução da equação de 2º grau.
Fórmula[editar]
Uma equação do segundo grau cujos coeficientes sejam números reais ou complexos possui duas soluções, chamadas de raízes da equação. As raízes são dadas pela seguinte fórmula:

sendo x, 'y e z os mesmos coeficientes da equação de segundo grau, e o símbolo ± indica que uma das soluções é obtida através da soma e a outra por meio da diferença.
A fórmula acima é utilizada para determinar as raízes de uma equação quadrática, isto é, os valores que a pode assumir. No Brasil, a fórmula é conhecida como Fórmula de Bhaskara, mas em outros países é conhecida simplesmente como a fórmula geral para resolução da equação polinomial do segundo grau,1 sem qualquer referência a Bhaskara, que foi um matemático e astrônomo indiano do século XII, e autor do livro Lilavat. A descoberta da fórmula costuma ser atribuída aos babilônios antigos, e sua formalização ao matemático persa Al-Khwarizmi[carece de fontes].
Demonstrações da fórmula quadrática[editar]
Durante longo tempo diversos estudiosos tentaram achar uma solução para x nesta equação, complicado por não haver um termo ao quadrado e o mesmo de segundo grau.[carece de fontes] Assim, a fórmula 1 de Bhaskara utiliza um método inteligente, unindo pura e simplesmente, uma fatoração de um polinômio para conseguir pôr apenas uma incógnita x no caso e assim, achar um valor negativo definitivo[carece de fontes]:
Se  então:
então:
 então:
então: |
Logo, tem-se, por definição de módulo, que:
Se  | Se  |
|---|---|
 |  |
Portanto,
 |
Ou:
 |
Discriminante[editar]
Na fórmula acima, a expressão que aparece sob a raiz quadrada é chamada de discriminante da equação quadrática, e é comumente denotada pela letra grega delta maiúsculo:

Dessa forma, pode-se reescrever a fórmula resumidamente como:

Uma equação quadrática com coeficientes reais tem duas raízes reais, ou então duas raízes complexas. O discriminante da equação determina o número e a natureza das raízes. Há apenas três possibilidades: (Lembrando que todo polinômio de grau n, tem n raízes; Como uma equação do 2º grau é de grau 2, logo ela possui duas raízes.)
- Se
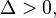 a equação tem duas raízes reais distintas.
a equação tem duas raízes reais distintas.- No caso de equações quadráticas com coeficientes inteiros, se o discriminante for um quadrado perfeito, então as raízes sãonúmeros racionais — em outros casos eles podem ser irracionais quadráticos.
- Se
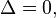 a equação tem duas raízes reais e iguais, ou popularmente "uma única raiz", algumas vezes chamada de raiz dupla:
a equação tem duas raízes reais e iguais, ou popularmente "uma única raiz", algumas vezes chamada de raiz dupla:
- Se
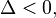 a equação não possui qualquer raiz real. Em vez disso, ela possui duas raízes complexas distintas, que são conjugadas uma da outra:
a equação não possui qualquer raiz real. Em vez disso, ela possui duas raízes complexas distintas, que são conjugadas uma da outra:
-

e 
- onde i é a unidade imaginária.
Assim as raízes são distintas se e somente se o discriminante é não nulo, e são reais se e somente se o discriminante é não-negativo.
Geometria[editar]
As soluções da equação quadrática
são também as raízes da função quadrática:
uma vez que elas são os valores de x para os quais
Se a, b, e c são números reais e o domínio de f é o conjunto dos números reais, então as raízes de f são exatamente as abcissas dos pontos nos quais o gráfico toca o eixo x.
Disto segue que, se o discriminante é positivo, o gráfico toca o eixo x em dois pontos, se for zero o gráfico toca em apenas um ponto e se for negativo, o gráfico não encosta no eixo x.
Forma fatorada da equação quadrática[editar]
O termo
é um fator do polinômio
se e somente se r é uma raiz da equação quadrática
Segue da fórmula quadrática que
No caso especial em que a quadrática possui apenas uma raiz ( isto é, discriminante nulo), o polinômio quadrático pode ser fatorado como
isto é, discriminante nulo), o polinômio quadrático pode ser fatorado como
 isto é, discriminante nulo), o polinômio quadrático pode ser fatorado como
isto é, discriminante nulo), o polinômio quadrático pode ser fatorado comoRelações entre coeficientes e raízes[editar]
As fórmulas de Viète fornecem uma relação simples entre as raízes de um polinômio e seus coeficientes. No caso do polinômio quadrático, elas tomam a seguinte forma
A partir de fórmula de Bhaskara, pode-se deduzir expressões bastante simples para a soma e para o produto das raízes 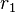 e
e 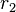 da equação:
da equação:
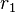 e
e 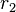 da equação:
da equação:
e
Estas igualdades seguem diretamente da relação:
que pode ser comparada termo a termo com:
Em alguns casos simples, o uso dessas propriedades permite que se deduza quais são as raízes, pela simples inspeção visual e tentativa de composição de dois números que satisfaçam as relações dadas para a soma e para o produto das raízes.
A primeira das duas fórmulas fornece também uma expressão conveniente ao traçar o gráfico de uma função quadrática. Uma vez que o gráfico é simétrico com relação a uma reta vertical passando pelo vértice da parábola, quando há duas raízes reais a abscissa do vértice está localizada na média aritmética das duas raízes, isto é, seu valor é dado pela expressão:
A outra coordenada pode ser obtida através da substituição do resultado anterior na expressão quadrática, resultando em
Assim, o gráfico da função  será sempre uma parábola com vértice em
será sempre uma parábola com vértice em
 será sempre uma parábola com vértice em
será sempre uma parábola com vértice em
Para um estudo mais detalhado do gráfico, ver função quadrática.
Em termos práticos, as fórmulas de Viète fornecem um método útil para a busca de raízes de uma quadrática no caso em que uma raiz é bem menor do que a outra. Se |x 1| << |x 2|, então x 1 + x 2 ≈ x 1, e tem-se a estimativa:
Da segunda fórmula de Viète resulta:
Estas fórmulas são mais fáceis de avaliar do que a fórmula de Bhaskara sob a condição de que uma raiz é grande e uma pequena, porque a fórmula de resolução de equações quadráticas avalia a raiz menor como a diferença entre dois numeros praticamente iguais (no caso em que b é grande), o que causa erros de arredondamento em avaliações numéricas. A figura ao lado mostra a diferença entre (i) um calculo direto usando a fórmula de Bhaskara (preciso quando as raízes têm valores próximos) e (ii) uma avaliação baseada na aproximação das fórmulas de Viète dadas acima (precisa quando as raízes estão bem separadas). Conforme o coeficiente linear baumenta, inicialmente a fórmula quadrática é precisa, e a a fórmula aproximada melhora sua precisão, levando a pequenas diferenças entre os métodos ao aumentar b. No entanto, em algum ponto a fórmula de Bhaskara começa a perder precisão devido aos erros de arredondamento, enquanto o método aproximado continua a melhorar. Consequentemente a diferença entre os métodos começa a aumentar ao paço que a fórmula de Bhaskara fica cada vez pior.
Esta situação aparece com frequência em design de amplificadores, onde raízes é desejável raízes bastante separadas para garantir uma operação estável.
Outras relações entre as raízes[editar]
Denotando-se as raízes de uma equação do segundo grau por 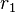 e
e  sua soma por
sua soma por  e seu produto por
e seu produto por  verificam-se as seguintes relações entre as raízes:
verificam-se as seguintes relações entre as raízes:
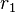 e
e  sua soma por
sua soma por  e seu produto por
e seu produto por  verificam-se as seguintes relações entre as raízes:
verificam-se as seguintes relações entre as raízes:| Expressão envolvendo as raízes | Definição | Relação com  e e  |
|---|---|---|
| Soma do inverso das raízes |  |  |
| Soma dos quadrados das raízes |  |  |
| Soma dos quadrados dos inversos das raízes |  |  |
| Soma dos cubos das raízes |  |  |
| Média aritmética das raízes |  |  |
| Média geométrica das raízes |  |  |
| Média harmônica das raízes |  |  |
Resolução das equações incompletas[editar]
c=0[editar]
É uma equação no formato  cuja solução pode ser obtida considerando-se que:
cuja solução pode ser obtida considerando-se que:
 cuja solução pode ser obtida considerando-se que:
cuja solução pode ser obtida considerando-se que:
De fato, neste caso tem-se necessariamente que  ou
ou  sendo esta última alternativa equivalente a
sendo esta última alternativa equivalente a  Em particular, se os coeficientes forem reais, as raízes também serão.
Em particular, se os coeficientes forem reais, as raízes também serão.
 ou
ou  sendo esta última alternativa equivalente a
sendo esta última alternativa equivalente a  Em particular, se os coeficientes forem reais, as raízes também serão.
Em particular, se os coeficientes forem reais, as raízes também serão.b=0[editar]
É uma equação no formato  que pode ser resolvida levando-se em conta que:
que pode ser resolvida levando-se em conta que:
 que pode ser resolvida levando-se em conta que:
que pode ser resolvida levando-se em conta que:
e que portanto,  ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.
ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.
 ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.
ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.

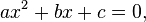





![ax^2+bx+c = a \left( x - \frac{-b + \sqrt {b^2-4ac}}{2a} \right) \left( x - \frac{-b - \sqrt {b^2-4ac}}{2a} \right) = a \left [(x - r_1)(x - r_2)\right ].](http://upload.wikimedia.org/math/6/7/3/673d7b7b2ac397cd6048c271fdf72b30.png)
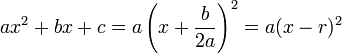




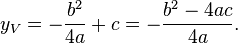






0 comentários:
Postar um comentário